Beliebige Dreiecke

Rechtwinklig? Egal!

Der Kosinussatz ist eine Erweiterung des Pythagoras-Satzes für beliebige Dreiecke, nicht nur für rechtwinklige. Er lautet:

$$ c^2 = a^2 + b^2 - 2ab \cdot \cos\gamma $$

Hierbei sind $a$, $b$ und $c$ die Seiten des Dreiecks und $\gamma$ der Winkel, der der Seite $c$ gegenüberliegt. Dieser Satz ermöglicht es, aus zwei Seiten eines Dreiecks und dem eingeschlossenen Winkel die dritte Seite zu berechnen.

Einen klassischen Beweis für den Kosinussatz kann man durch Zerlegung des Dreiecks und Anwendung des Pythagoras-Satzes führen. Hier ist eine einfache Version des Beweises:

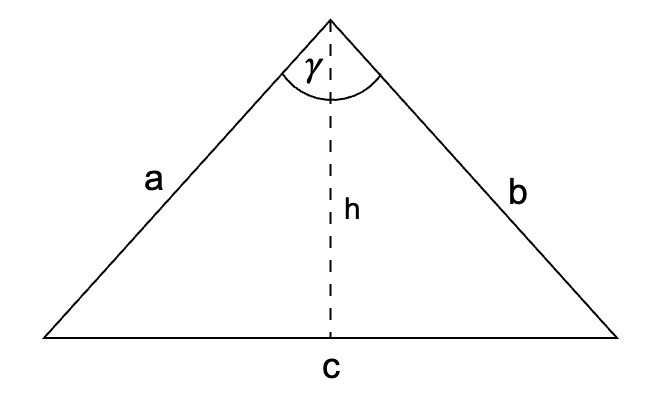
Dreieck und Notation: Betrachte ein beliebiges Dreieck $\triangle ABC $ mit Seiten $a$, $b$ und $c$ und Winkeln $\alpha$, $\beta$, und $\gamma$ gegenüber den Seiten $a$, $b$, und $c$ entsprechend. Projiziere die Seite $b$ auf die Seite $c$, wodurch der Punkt $D$ auf $c$ so entsteht, dass $AD$ senkrecht zu $c$ steht. Die Länge der Projektion von $b$ auf $c$ ist $b \cos\gamma$. Das Dreieck $ \triangle ABC $ wird durch $AD$ in zwei rechtwinklige Dreiecke $ \triangle ABD $ und $ \triangle ADC $ zerlegt.

Anwendung des Pythagoras-Satzes: Im Dreieck $ \triangle ABD $ gilt:

$$ AB^2 = AD^2 + BD^2 $$

Wobei $BD = b \cos\gamma$ und $AB = c$.

Länge von $AD$: Da $AD$ die Höhe ist, gilt auch:

$$ AD = b \sin\gamma $$

Nutze diese Information und setze sie in die Pythagoras-Gleichung ein:

$$ c^2 = (b \sin\gamma)^2 + (b \cos\gamma)^2 $$

Vereinfache weiter unter Nutzung der trigonometrischen Identität $ \sin^2\gamma + \cos^2\gamma = 1 $:

$$ c^2 = b^2 (\sin^2\gamma) + \cos^2\gamma = b^2 $$

Endgültige Formulierung: Füge die Projektion $AC$ hinzu:

$$ AC = c - b \cos\gamma $$

Nun wende den Pythagoras-Satz im Dreieck $ \triangle ADC $ an:

$$ a^2 = AC^2 + AD^2 $$

Setze $AC$ und $AD$ ein:

$$ a^2 = (c - b \cos\gamma)^2 + (b \sin\gamma)^2 $$

Führe die Quadrierung und Vereinfachung durch:

$$ a^2 = c^2 - 2bc \cos\gamma + b^2\cos^2\gamma + b^2\sin^2\gamma $$

Und da $\sin^2\gamma + \cos^2\gamma = 1$, ergibt sich:

$$ a^2 = c^2 + b^2 - 2bc \cos\gamma $$

180° oder doch nicht?

Aus der Schule erinnern wir uns, dass die Summe der Winkel im Dreieck 180° betragen soll. Das ist sicher erstmal richtig:

Beweis

Gegeben sei ein Dreieck $\triangle ABC$ mit den Innenwinkeln $\alpha, \beta, \gamma$. Wir ziehen eine Gerade durch $A$, so dass diese senkrecht zu $BC$ steht. wir erhalten neue Winkel $\delta = \gamma$ und $\epsilon = \beta$.

Die Summe der Winkel an einer Geraden ist logischerweise 180°, somit ergibt sich

$$ \alpha + \delta + \epsilon = 180^\circ $$

Mit $\delta = \gamma$ und $\epsilon = \beta$ kommt man auf

$$ \alpha + \gamma + \beta = 180^\circ, $$

was zu zeigen war.

Jetzt stellen wir uns aber ein grosses Dreieck vor, das beispielsweise seine Ecken in Lissabon, Peking und Reykjavik hat. Wenn wir mit Karte und Kompass nun den Kurs bestimmen und am Ende der Reise den jeweiligen Kurs addieren, werden wir auf wesentlich mehr als 180° kommen. Anhand eines rechtwinkligen Beispiels kann man das noch schöner sehen: Geht man vom Nordpol genau nach Süden, biegt dann am Äquator nach Westen ab und nach einem Viertel des Umfangs¹ wieder genau nach Norden, hat man ein Dreieck, dessen Winkel alle 90° sind, also die Winkelsumme 270° beträgt. Wie man sich leicht klarmachen kann, ist dort das Ende nicht erreicht.

Das liegt natürlich daran, dass die Dreiecke nicht mehr in der Ebene liegen und wir eine andere Art von Geometrie anwenden müssen, die so genannte sphärische Geometrie. Auf der Kugeloberfläche können wir die Seitenlänge von Dreiecken als Winkel angeben, was die Umrechnung von geografischen Koordinaten erheblich vereinfacht.

Wir lassen also die Euklidische Geometrie hinter uns, die uns über zweitausend Jahre gute Dienste geleistet hat und sprechen von einem Eulerschen Dreieck².

Die Summe der Winkel ist dabei abhängig von der Fläche des Dreiecks und dem Radius der Kugel:

$$\alpha + \beta + \gamma = \frac{A}{r^2} + \pi $$